다익스트라 알고리즘이란 ?
음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 구하는 알고리즘입니다. 도착 정점 뿐만아니라 모든 다른 정점까지 최단 경로로 방문하며, 각 정점까지의 최단 경로를 모두 찾게 됩니다. 매번 최단 경로로 정점을 선택해 탐색을 반복하는 것 입니다.
음의 간선이 존재하지 않기 때문에 다익스트라는 현실세계에 사용하기 매우 적합한 알고리즘 중 하나입니다. 이 알고리즘은 다이나믹 프로그래밍을 활용하였는데, 그 이유는 '최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문'입니다. 하나의 최단거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있습니다.
동작 과정
1. 출발 노드를 설정합니다.
2. 출발 노드를 기준으로 각 노드의 최소 비용을 저장합니다.
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택합니다.
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신합니다.
5. 위 과정에서 3~4번을 반복합니다.

위와 같이 그래프가 있다면, 아래와 같은 자료구조 형태로 처리해야 합니다. 아래 표의 의미는 특정 행에서 열로 가는 비용을 나타냅니다. 예를 들어 1행 3열의 값이 5라면, 1번 노드에서 3번 노드로 가는 비용이 5라는 의미입니다.
|
0
|
2
|
5
|
1
|
무한
|
무한
|
|
2
|
0
|
3
|
2
|
무한
|
무한
|
|
5
|
3
|
0
|
3
|
1
|
5
|
|
1
|
2
|
3
|
0
|
1
|
무한
|
|
무한
|
무한
|
5
|
1
|
0
|
2
|
|
무한
|
무한
|
5
|
무한
|
2
|
0
|
이 상태에서 1번 노드를 선택합니다.

위와 같이 노드를 선택한 상태이고, 그와 연결된 세 개의 간선을 확인한 상태라고 할 수 있습니다. 1번 노드에서 다른 정점으로 가는 최소 비용은 다음과 같습니다. 배열을 만든 뒤에는 이 최소비용 배열을 계속해서 갱신할 것입니다. 현재 방문하지 않는 노드중에서 가장 비용이 적은 노드는 4번 노드 입니다.
|
0
|
2
|
5
|
1
|
무한
|
무한
|
따라서 위 배열의 상태를 고려하여 4번 노드가 선택이 되었습니다. 4번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열을 갱신하면 됩니다.

기존에 5로가는 최소 비용은 무한이었습니다. 하지만 4를 거쳐서 5로 가는 경우는 비용이 2이므로 최소비용 배열을 갱신해 줍니다. 또한 4를 거쳐서 3가는 경우는 비용이 4이므로 기존보다 더 저렴합니다. 따라서 최소 비용 배열을 갱신해줍니다.
|
0
|
2
|
4
|
1
|
2
|
무한
|
이제 다음으로 방문하지 않은 노드중에서 가장 비용이 적은 노드는 2번 노드입니다.

보면 2를 거쳐서 가더라도 비용이 갱신되는 경우가 없습니다.따라서 배열은 그대로 유지합니다.
|
0
|
2
|
4
|
1
|
2
|
무한
|
다음으로 방문하지 않은 노드 중에서 가장 비용이 적은 노드는 5번째 노드입니다.
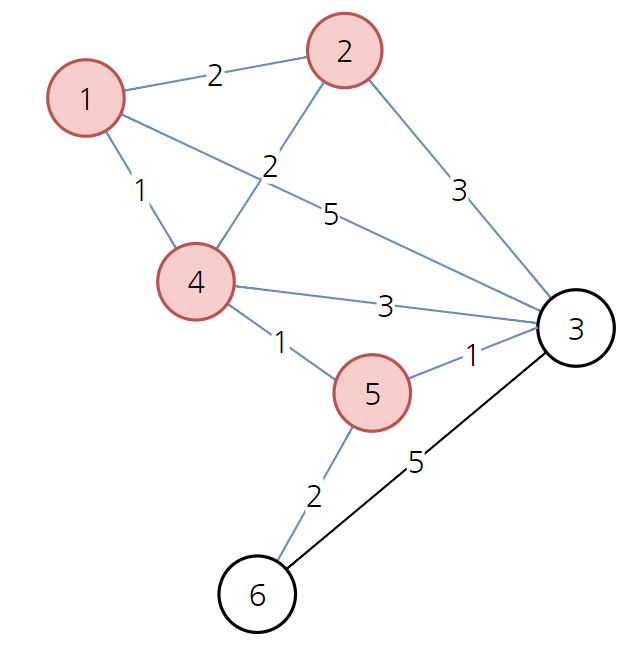
위와 같이 5를 거쳐서 3으로 가는 경우 경로의 비용이 3이므로 기존의 4보다 더 저렴합니다. 따라서 노드 3으로 가는 비용을 3으로 바꾸어주시면 됩니다. 또한 5를 거쳐서 6으로 가는 경우 경로의 비용이 4로 기존의 무한보다 더 저렴합니다. 따라서 노드 6으로 가는 비용을 4로 바꾸어주시면 됩니다.
|
0
|
2
|
3
|
1
|
2
|
4
|
이후에 방문하지 않은 노드 중에서 가장 저렴한 노드 3을 방문합니다.

최소 비용 갱신은 일어나지 않습니다.
|
0
|
2
|
3
|
1
|
2
|
4
|
이제 마지막으로 남은 노드 6을 살펴봅시다.

노드 6을 방문한 뒤에도 결과는 같습니다. 따라서 최종 배열은 다음과 같이 형성됩니다.
|
0
|
2
|
3
|
1
|
2
|
4
|
코드 구현 in Javascript
단순 반복문을 사용하여 O(N^2)의 시간복잡도를 갖는 구현법이 있으며, 힙 자료를 사용하는 우선순위 큐로 구현한 O(NlogN)의 시간복잡도를 갖는 구현법이 있습니다. 아래에는 미리 구현했었던 우선순위 큐를 활용하여 구현한 코드입니다.
class Node {
constructor(val, priority) {
this.val = val;
this.priority = priority;
}
}
class PriorityQueue {
constructor() {
this.values = [];
}
enqueue(val, priority) {
let newNode = new Node(val, priority);
this.values.push(newNode);
this.bubbleUp();
}
dequeue() {
const min = this.values[0];
const end = this.values.pop();
if (this.values.length > 0) {
this.values[0] = end;
this.bubbleDown();
}
return min;
}
bubbleUp() {
let idx = this.values.length - 1;
const element = this.values[idx];
while (idx > 0) {
let parentIdx = Math.floor((idx - 1) / 2);
let parent = this.values[parentIdx];
if (element.priority >= parent.priority) break;
this.values[parentIdx] = element;
this.values[idx] = parent;
idx = parentIdx;
}
}
bubbleDown() {
let idx = 0;
const length = this.values.length;
const element = this.values[0];
while (true) {
let leftChildIdx = 2 * idx + 1;
let rightChildIdx = 2 * idx + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIdx < length) {
leftChild = this.values[leftChildIdx];
if (leftChild.priority < element.priority) {
swap = leftChildIdx;
}
}
if (rightChildIdx < length) {
rightChild = this.values[rightChildIdx];
if (
(swap === null && rightChild.priority < element.priority) ||
(swap !== null && rightChild.priority < leftChild.priority)
) {
swap = rightChildIdx;
}
}
if (swap === null) break;
this.values[idx] = this.values[swap];
this.values[swap] = element;
idx = swap;
}
}
}
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
addEdge(vertex1, vertex2, weight) {
this.adjacencyList[vertex1].push({ node: vertex2, weight });
this.adjacencyList[vertex2].push({ node: vertex1, weight });
}
Dijkstra(start, finish) {
const nodes = new PriorityQueue();
const distances = {};
const previous = {};
const path = [];
let smallest;
// build up initial state
for (let vertex in this.adjacencyList) {
if (vertex === start) {
distances[vertex] = 0;
nodes.enqueue(vertex, 0);
} else {
distances[vertex] = Infinity;
nodes.enqueue(vertex, Infinity);
}
previous[vertex] = null;
}
while (nodes.values.length) {
smallest = nodes.dequeue().val;
if (smallest === finish) {
while (previous[smallest]) {
path.push(smallest);
smallest = previous[smallest];
}
break;
}
if (smallest || distances[smallest] !== Infinity) {
for (let neighbor in this.adjacencyList[smallest]) {
let nextNode = this.adjacencyList[smallest][neighbor];
let candidate = distances[smallest] + nextNode.weight;
if (candidate < distances[nextNode.node]) {
distances[nextNode.node] = candidate;
previous[nextNode.node] = smallest;
nodes.enqueue(nextNode.node, candidate);
}
}
}
}
return path
}
}
'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] 분할 정복(Divide and Conquer) (0) | 2023.02.28 |
|---|---|
| [Algorithm] 슬라이딩 윈도우(Sliding Window) (0) | 2023.02.16 |
| [Algorithm] 투 포인터(Two Pointer) (0) | 2023.02.15 |
| [Algorithm] Big-O 관점에서의 배열과 객체 (0) | 2023.02.13 |
| [Algorithm] Big-O-Notation (0) | 2023.02.12 |